Problemas de Refuerzo y Profundización

Problemas de Refuerzo y Profundización

Problemas de Refuerzo

Problema 1.

Desde un faro colocado a 40m sobre el nivel del mar se observa un barco con ángulo de inclinación depresión de 55° ¿a qué distancia se halla el faro del barco?

Problema 2.

Desde un faro de 32,4 m de altura se observa un barco con un ángulo de depresión de 41°. Desde otro faro. De 44,7 m de altura, se observa el mismo barco con un ángulo de depresión de36°.

·         Si los dos faros y el barco están alineados, y el barco está en medio, ¿Cuál es la distancia entre los faros?

·         Formula una pregunta que se pueda responder con los datos iniciales, si los dos faros y el barco no están alineados.

Problema 3.

Desde una torre de vigilancia en una playa, un salvavidas observa una boya en el mar con un ángulo de depresión de 3°. Si la observación se hace desde una altura de 4,5 m ¿a qué distancia esta la bolla de la torre?

Problema 4.

Miranda ve la copa de un árbol con ángulo de elevación de 65°. La situación se representó en la figura. ¿Cuál es la altura del árbol?

Problema 5.

Al moverse un péndulo de 100m de longitud forma un ángulo de 36° con la vertical. ¿Qué distancia sube el extremo inferior del péndulo respecto a la horizontal?

Problema 6.

En un triángulo isósceles, el ángulo determinado por los lados congruentes mide 80° y el lado opuesto a este ángulo mide 16m. ¿cuál es la medida de la altura sobre ese lado?

Problema 7.

Determina el ángulo de elevación del sol, si una persona de 1,70 m de altura produce una sombra de 1,50 m de longitud en el suelo.

Problema 8.

El cordel de una cometa se encuentra tenso y forma un ángulo de 60° con la horizontal. Determina la altura aproximada de la cometa respecto al suelo, si el cordel mide 70 m y el extremo de la cuerda se sostiene a 1,20 m del suelo.

  

Problema 9.

Un camino tiene una inclinación de 12° con respecto a la horizontal. ¿Cuánto se debe caminar hacia arriba para alcanzar un a altura de 40m?

Problema 10.

Una escalera de 12 m de longitud esta recostada sobre la pared vertical de un edificio. Si el ángulo entre la escalera y la pared es de 25°, ¿a qué distancia de la pared se encontrará la parte inferior de la escalera? Supongamos que la distancia hallada se incrementa en 1,20 m. ¿Qué longitud o distancia desciende la parte superior de la escalera?

Problemas de Profundización

Problema 11.

Un topógrafo que se encuentra en el fondo de una zanja es de 25°30’. Si el topógrafo está a 4 m de la base, ¿cuál es la profundidad de la zanja?

Problema 12.

Una antena de TV está instalada en el techo de una casa que tiene 5 m de altura. Desde un punto P en el suelo, situado a 40 m del punto que se encuentra directamente debajo de la antena, esta subtiende un ángulo de 15°. Calcula la atura de la antena.

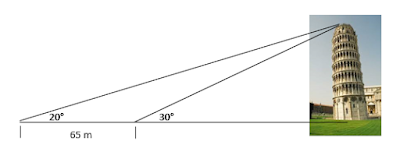
Problema 13.

Un topógrafo desea medir la altura de una torre situada en la ribera opuesta de un rio sin necesidad de atravesarlo. Para tal fin, coloca un teodolito en cierto punto P, de tal manera que la horizontal coincide con el pie de la torre, y mide un ángulo de elevación de 20°. Camina 65m en línea recta hacia el pie de la torre y, haciendo coincidir nuevamente la horizontal con dicho pie, mide un ángulo de elevación de 30°. ¿Cuál es la altura de la torre?

Problema 14.

Desde el punto P a 9m del suelo, el ángulo de elevación al punto más alto de un edificio es de 30°25’ y el ángulo de depresión a la base del mismo es de 15°45’. Calcula la altura del edificio.

Problema 15.

Desde un globo H, ubicado a 42 m sobre el nivel del mar, se observa una gaviota G, que está a 20 m del globo, con un ángulo de elevación de 7°. En la vertical de la gaviota hay un pez P a 8 m bajo el nivel del mar (ver figura) ¿Cuál es la distancia entre la gaviota y el pez?

Problema 16.

Si en un túnel que desciende con un ángulo de 15° respecto al nivel del suelo, una persona avanza una distancia de 75 m, ¿a qué distancia se encuentra dicha persona de la superficie?

Problema 17.

Desde un punto P del suelo, el ángulo de elevación a la cúspide de una torre – punto más alto- es de 30°25’. Desde otro punto 20 m más cercano a la torre, y en línea recta con el punto P y con la base de la torre, el ángulo de elevación a la cúspide es 60°50’. Calcula la altura de la torre.

Problema 18.

Una escalera de 10 m de longitud, como la que utilizan los bomberos, se ha fijado en un punto de la calle. Si se apoya sobre una de las fachadas forma un ángulo de 45° con el suelo, y se apoya sobre otra fachada del otro lado de la calle forma un ángulo de 30°. Halla el ancho de la calle. ¿Qué altura se alcanza con esta escalera sobre cada una de las fachadas?

Problema 19.

Desde un árbol, Antonio observa un caballo que se encuentra a 20 m del árbol. Luego, el caballo se mueve sobre al horizontal ubicándose a 15 m del árbol. ¿En cuál de los dos casos el ángulo de depresión con el que ve Antonio al caballo es el mayor? Justifica tu respuesta.

Problema 20.

El piloto de un avión que vuela a 2000 m de altura divisa una ciudad de destino con un ángulo de depresión de 15°. ¿a qué distancia x está la ciudad?

Problema 21.

Un avión vuela entre dos ciudades, A y B, que distan 80 km. Las visuales desde el avión a A y a B forman ángulos de 29° y 43° con la horizontal, respectivamente. ¿A qué altura está el avión?

Problema 22.

La distancia entre 2 puntos A y B es de 20 km. Los ángulos de elevación de un globo con respecto a dichos puntos son de 58°20’ y 67°32’. ¿A qué altura del suelo se encuentran?   

Problema 23.

Dos antenas de radio están sujetas al suelo por cables tal como lo indica la figura. Calcula la longitud de cada uno de los tramos de cable y la distancia AE.

Problema 24.

Dos edificios distan entre sí 150 m. Desde un punto del suelo que está entre los dos edificios, vemos que las visuales a los puntos más altos de estos forman con la horizontal ángulos de 35° y 20°. ¿Cuál es la altura de los edificios, si sabemos que los dos miden los mismo?

Problema 25.

Una escalera para acceder a un túnel tiene la forma y las dimensiones de la figura, calcula la profundidad del punto B